【確率】複勝式馬券の当たる確率【数学#3】

数学の第３回は、確率。
今回は、複勝式馬券の当たる確率について、中学生でも理解できるよう分かりやすく解説していきます。

複勝式馬券の当たる確率は計算できるのか？

数学の第１回では、単勝式馬券の当たる確率について解説しました。その時の結論は何だったかというと、「単勝式馬券の当たる確率を正確に計算する数式は存在しない」というものでした。

その理由は、どの競馬レースでも各出走馬が勝つ能力は同様に確からしくないこと、言い換えると、レースに勝つ確率は馬ごとにバラバラであることです。
詳しくは以下の記事をご覧ください。

では、複勝式馬券についてはどうかというと、当然ながら、単勝式であろうと複勝式であろうと賭けの対象が競馬レースであることに変わりはありませんので、「複勝式馬券の当たる確率も正確に計算する数式は存在しない」という結論になります。

しかし、それで終わってしまっては「競馬の本質」を理解する上で不十分ですので、本記事ではあえてどの馬もレースを勝つ能力が「同様に確からしい」と仮定した場合の確率を求めて見ます。

「同様に確からしい」場合の複勝式馬券の当たる確率

ここであらためて「同様に確からしい」という意味について説明します。

例えば、サイコロを振って１から６までのどの目が出るかという確率を考えると、どの目の出方も確率は等しいと考えられますので、それぞれ６分の１の確率で目が出てくる、と計算できます。
この「（サイコロの）どの目の出方も確率は等しいと考えられる」ということを「同様に確からしい」と言います。

競馬レースにおいて「同様に確からしい」と仮定することは、すなわち「どの馬にも等しくレースを勝つ能力がある」と仮定することですので、いかにこの仮定が現実とかけ離れているのか、馬券が得意な皆様にはご理解いただけるのではないでしょうか。

一方で、競馬初心者の方や馬券が苦手な方にとっては、この仮定が馬券を買う上でどれだけ致命的な間違いなのかピンときていない可能性があります。
この記事の目的は、この馬券の”落とし穴”に気づくことで、どのようなスタンスで馬券と向き合うべきか考えるきっかけを作ることにあります。

では早速ですが、基本的な確率の求め方（計算式）を以下に示します。

先ほどのサイコロの例でいうと、出目のパターンは全部で６通り(n=6）あって、１から６までの目が出るパターンは１通りずつ（a=1）しかないので、それぞれの目が出る確率は等しく６分の１（1÷6）ということになります。

１着馬を当てる単勝式の場合、的中となる馬券のパターンは１通り（a=1）しかありませんので（１着同着の場合を除く）、１を出走頭数（n）で割れば簡単に確率が計算できます（例：18頭立てのレースなら18分の１）。
一方で、複勝式は１着から３着までに入る馬を当てる馬券ですので、計算は少し複雑です。
複勝式については、以下の記事で詳しく解説しています。

すなわち、複勝式馬券の当たる確率を求めるには、１着から３着までの組み合わせが全体で何通りあって、そのうち実際に的中となる馬券のパターンが何通りあるのかを調べる必要があります。

では、まず１着から３着までの組み合わせが全体で何通りあるのかを調べるための計算式を以下に示します。

例えば、10頭立てのレース（n=10）の場合、１着から３着までの組み合わせは、10 × 9 × 8 ＝ 720（通り）という計算になります。
「え？そんなに多いの？」と思われた方もいるかもしれませんが、例えば馬番①～③の３頭が上位３着までに入った場合だけを考えてみても、①-②-③というパターンだけでなく、①-③-②、②-①-③、②-③-①、③-①-②、③-②-①という計６通りものパターンがあるわけです。
これを全10頭に広げて計算すれば、結果的に720通りまでパターンが膨れ上がるわけです。
これは高校数学で習う「順列」というものですが、この教材はあくまで中学生向けですので、「こういう計算式なんだ」という程度にご理解ください。

続いて、１レースあたりの複勝式馬券の的中パターンが何通りあるか調べるための計算式を以下に示します。

例えば、10頭立てのレース（n=10）の場合、馬１頭あたりの複勝式馬券の的中パターンは、3 × 9 × 8 ＝ 216（通り）という計算になります。
これも「え？そんなに多いの？」と思う人が多いかもしれません。
しかしよく考えれば、選んだ馬が１着に入ったとすると、２着から３着までにはどんな馬が入っても的中となるわけですから、それだけで9×8=72（通り）。これが２着に入った場合も３着に入った場合も同様に的中となるので、72×3=216（通り）という計算になるわけです。

なお、上の複勝式に関する記事のとおり、出走頭数が７頭以下のレースについては１着または２着の馬を当てた場合にのみ的中となるため（３着の馬は外れ）、上記の計算式はあくまで出走頭数が８頭以上（n>7）のレースにのみ適用できます。

以上を踏まえて、複勝式馬券の当たる確率を求めると、以下のような計算式になります。

というわけで、複勝式馬券の当たる確率は 3/n という非常にシンプルな式で計算できることがわかります。
ここで思い出してみましょう。
単勝式馬券の当たる確率の計算式は1/nでしたね。
そうです。複勝式馬券の当たる確率は、単勝式馬券の当たる確率のちょうど３倍になるのです。

あらためて確率を計算しなくても、単勝式は１着に入った場合だけが的中で、複勝式は１着から３着までに入れば的中になるのですから、複勝式のほうが当たる確率が３倍高いことは簡単に想像できたでしょう。
数学的にもこの想像が正しかったことを証明できたわけですが、忘れてはならないのは、あくまでどの馬もレースを勝つ能力が等しい（同様に確からしい）と仮定した場合の話だということです。

本当に単勝式よりも複勝式のほうが３倍も当たるのか？

冒頭の結論に戻りますが、どの馬もレースを勝つ能力が等しいなどということはあり得ませんので、単勝式馬券と同様に、複勝式馬券の当たる確率も正確に計算する数式は存在しないのです。

では、複勝式のほうが単勝式よりも３倍も当たる確率が高いという計算は間違っているのでしょうか？

ここからは、実際の競馬データを使って先ほどまでの仮定と計算式が間違っているのかどうか検証してみます。

以下は、2015年から2024年までの10年間に東京競馬場の芝1,600mで開催された18頭立てレースの全データ（計160レース）を集計したものです。
※データ集計にはJRA-VANアプリ「TARGET frontier JV」を使用

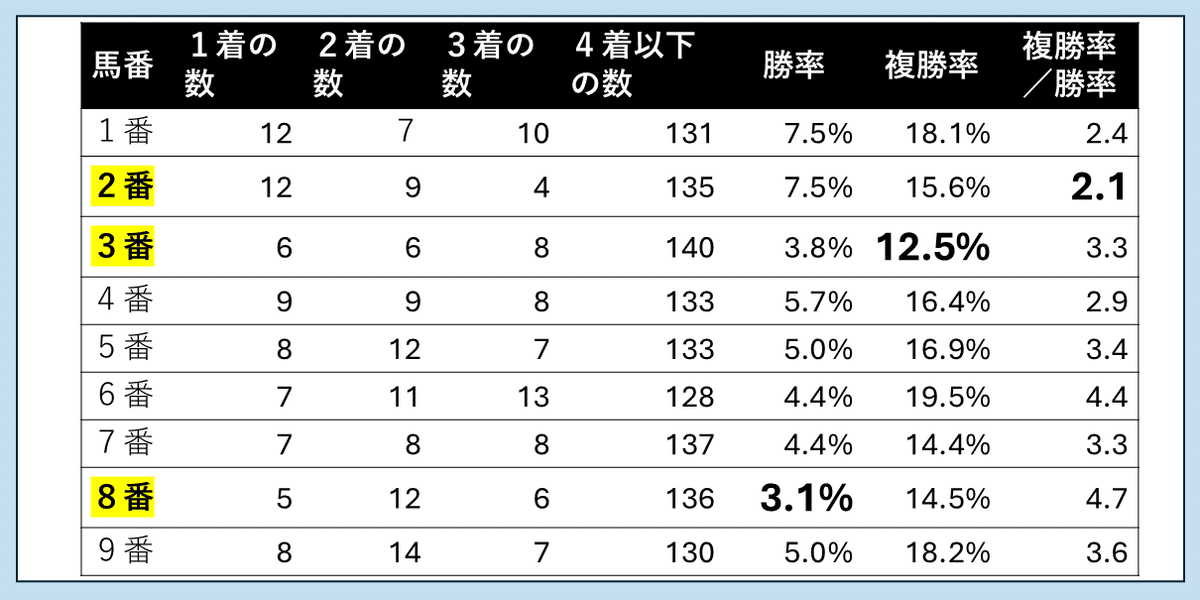
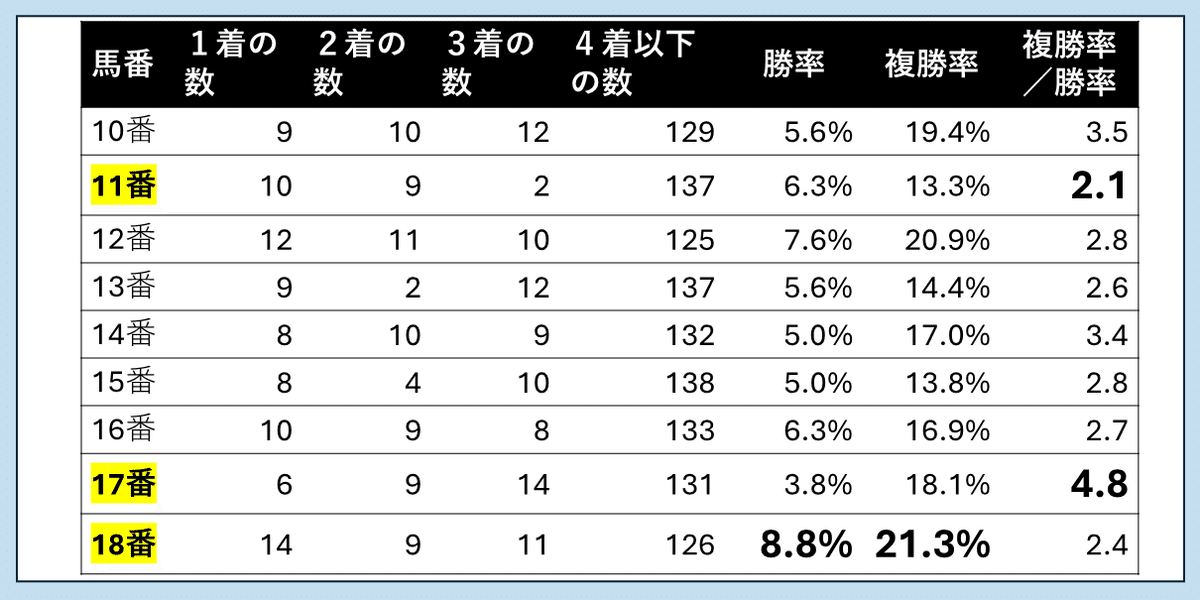
上の表で示したデータでは、馬番ごとに１着馬の頭数、２着馬の頭数、３着馬の頭数、４着以下の馬の頭数を集計していて、さらに全体の頭数に対する１着馬の割合を「勝率」として、同じく１着から３着までに入った馬の割合を「複勝率」として表しています。
すなわち、勝率は単勝式馬券の当たる確率を、複勝率は複勝式馬券の当たる確率を示しているのです。

例えば、全160レースで馬番１番の単勝式馬券だけ買い続けた場合、１番の勝率は7.5%ですので、7.5%の確率で馬券が的中することになります。
また同じように馬番１番の複勝式馬券だけ買い続けた場合、１番の複勝率は18.1%ですので、18.1%の確率で馬券が的中するというわけです。

仮に全ての馬に等しく勝つ能力がある（同様に確からしい）とすると、18頭立てレースにおける単勝式馬券の当たる確率は18分の１（5.6%）、複勝式馬券の当たる確率は18分の３（16.7%）と計算できます。
ところが、上の表を見ていただければ、この計算上の確率が実際の競馬データには全く合致しないことがご理解いただけるでしょう。

中には近いデータもありますが（10番の勝率、５番の複勝率など）、例えば８番の勝率は3.1%なのに対して、18番の勝率は8.8%と２倍以上の開きがあります。つまり、８番の単勝式を買い続けるよりも、18番の単勝式を買い続ける方が２倍以上も当たる確率が高いのです。
複勝率に関しても、３番の複勝率は12.5%なのに対して、18番の複勝率は21.3%と大きく異なっています。
しかも、18番の馬に関しては勝率、複勝率ともにトップの成績になっていますので、「東京芝1,600mのレースは確率的に18番の馬を買うべき」ということすら言えるわけです。

なぜ18番の馬は馬券に絡む確率が高いのか？
その理由は良く分かりませんが、サンプル数が少ないことから偶然の結果であることも否定はできません。また、他のレース条件―違う競馬場や違う距離など―では全くことなる結果になることも十分考えられます。
いずれにしても、10年間同じ条件のレースを買い続ける場合でもこのような確率のバラつきが生まれるわけですから、少なくともファンの皆様が現役で馬券を買い続けている間にこの確率のバラつきがなくなることはないでしょう。

さて、単勝式よりも複勝式のほうが３倍も当たるのかどうかについてですが、上の表の一番右の欄に馬番ごとの勝率と複勝率の比を示しています。
この数値（比）は、その馬番の複勝率が勝率の何倍にあたるのか、すなわち、複勝式が単勝式より何倍当たる確率が高いのかを表しているわけですが、これもかなりのバラつきがあることがわかります。
確かに３倍前後の数字が多いのですが、２番が2.1倍なのに対して、17番は4.8倍と２倍以上の開きがあります。
17番に関しては、単勝式を買わずに複勝式を買う方が賢明かもしれません。

単勝式よりも複勝式のほうが当たる確率が高いことに間違いはありません。
重要なことは、１着に入る（単勝式が当たる）確率が高い馬が、必ずしも２着や３着に入る（複勝式が当たる）確率が高くなるわけではないし、その逆もまた然り、ということです。
「ピンかパーか（一か八か）」という表現を競馬で使うことがありますが、勝つときはあっさり勝つのに、負ける時は「えっ？」と思うような惨敗をする馬も少なくありません。
逆に、なかなか１着は獲れないのに、いつも２着や３着には入ってくる「シルバー（ブロンズ）コレクター」と言われる馬たちもいます。

いずれにしても、これらの馬の馬券が当たる確率を正確に計算する計算式はありません。
先ほどのデータで示したような過去のレース傾向や各馬の特徴などを踏まえて、どの馬券の買い方が一番当たる確率が高くなるのかを競馬ファンが自ら研究、推定するしか馬券を当てる方法はないということです。

参考書籍

「やさしい中学数学　改訂版　電子版」（きさらぎひろし著、Gakken）