【１次関数】単勝式と複勝式を同時に買う場合のベストな資金配分【数学#4】

数学の第４回は、１次関数。
今回は、「単勝式と複勝式を同時に買う場合のベストな資金配分」について、中学生でも理解できるよう分かりやすく解説していきます。

単複の資金配分に関する一般的な見解

単勝式と複勝式（以下まとめて「単複」といいます）の当たる確率については、それぞれ以下の記事で解説しました。

結論は、いずれの馬券の買い方も（というか、全ての馬券の買い方が）当たる確率を正確に算出する数式は存在しない、というものでした。
すなわち、どの馬がどのくらいの確率で勝ちそうか（または３着以内に入りそうか）ということを様々な要素から推定することが、馬券の本質であるということです。

さて、あるレースの出走馬について各馬の勝つ確率を全て推定できたとして、最も勝つ確率が高そうな馬の単複を同時に買いたい場合は、それぞれの買い方にどのくらいの比率でお金を賭ければ（以下「資金配分」といいます）効率よく資金を回収できるのでしょうか？

当然ながら、単勝式よりも複勝式の方が当たりやすいのですが、その反面、同じ金額をかけた時の払戻金は単勝式よりも複勝式の方が少なくなります。なぜなら、単勝式のオッズよりも複勝式のオッズの方が圧倒的に低く設定されるためです。
詳しくは、以下の記事で解説しています。

ですから、複勝式の方にたくさんのお金を賭けたくなりますが、そうすると単勝式に賭けるための予算（資金）が減ってしまい、単勝式が当たった時の払戻金は減ってしまいます。
単勝式が当たるということは、同時に複勝式も当たることを意味していますので（同じ馬を買っているのに単勝式だけ当たって複勝式が外れることなどあり得ません）、複勝式を保険的に少額賭けて単勝式の方により多くのお金を賭けたくもなります。しかし、もし馬券を買った馬が２着や３着だった場合（単勝式が外れて複勝式だけ当たった場合）には、複勝式だけでは賭けたお金の全額を回収できず、収支はマイナス（赤字）になってしまいます。

競馬予想を扱ったネット記事を検索してみると、単複の理想的な資金配分について以下のような見解が見つかりました。

穴狙いの人だと2:8で、平均すると3:7くらいでかけてる人が多いです

「ゆしろう式買い方講座」https://note.com/yushiro__/n/n6189142a2333より

単複バランス法は、単勝に30％、複勝に70％のバランスで馬券を購入します

「競馬単複必勝法で絶対に勝つ！【単複バランス法で稼ぐ】」https://www.yumetoniji.com/より

単勝：複勝の黄金比は単勝１に対して複勝は３以上。単勝：複勝１：２はおすすめできない！

「イッコバ（北の競馬王）の馬券道」の「【馬券　単複】勝てる単複の黄金比はこれだ！単複の魅力と極意！」https://www.kitanokeibao.blog/?p=1012#%E5%8D%98%E8%A4%87%E3%81%AE%E9%BB%84%E9%87%91%E6%AF%94%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6%E3%81%AE%E8%80%83%E5%AF%9Fより

単勝式と複勝式の配分比率は、単勝式１に対して複勝式２～４くらいが一般的に良いとされているようです。

しかし、レースによってオッズはまちまちですし、馬券を買いたい馬が人気馬か穴馬（不人気馬）かによっても理想的な資金配分は変わってくるわけですから、同じ比率を全てのレースに一律に当てはめることは回収率（賭けた金額に対して何%が払戻金として回収できたか）の低下につながります。

そこで、より多くの払戻金が得られ、かつ、赤字（マイナス収支）を防ぐことができるような理想的な資金配分を、中学校レベルの数学を使って計算してみよう、というのが今回の記事の趣旨です。

１次関数を使って資金配分を考える

では、どんな中学レベルの数学を使うのかというと、１次関数です。

ちなみに、「関数」とは次のような意味です。

かん すう［関数・函数］（名）
ある数〔=y〕がほかの数〔=x〕の変化にしたがって変化するとき、xに対するyの呼び名。「yはxの関数」と言う。

「三省堂国語辞典　第七版」より

１次関数とは、関数のうち以下の式で表されるものを言います。

思い出してきましたか？
aとbは定数（決まった数字）で、aのことを「係数（けいすう）」とか「傾き（かたむき）」と言い、bのことを「切片（せっぺん）」と言います。

では、単複の資金配分と１次関数がどう関係してくるのか、これから説明していきます。

まず、１つのレースで１頭分の単複を購入することを考えてみます。
現実の競馬では「１頭分しか買ってはならない」というルールはないですし、単複とその他の買い方を併用して馬券を買うこともできるのですが、問題を単純化するためにあえてこのような設定としています。

例えば、資金がb円あって、そのうちx円を単勝式に、y円を複勝式に配分して馬券を買う場合、以下のような式が成り立ちます。

当たり前ですが、単勝式に充てる資金(x)と複勝式に充てる資金(y)を足した金額が資金の総額(b)となります。

・・・何となくわかってきましたね。
そうです。この数式を変換すれば１次関数の式（以下のとおり）になるのです。

つまり、複勝式に賭けるy円は、単勝式に賭けるx円の１次関数なんです。

よく考えてみれば当たり前ですよね。１レースあたりに賭けることができる金額の上限（資金）は決まっているのですから、そのうち単勝式にいくら賭けるかによって、必然的に複勝式に賭けられる金額も決まってくるわけです。このことをあえて「関数」と表現しているに過ぎません。

グラフを使って資金配分を考える

次に、単複のベストな資金配分を考えるために、先ほどの１次関数の式を使ってグラフを描いてみます。

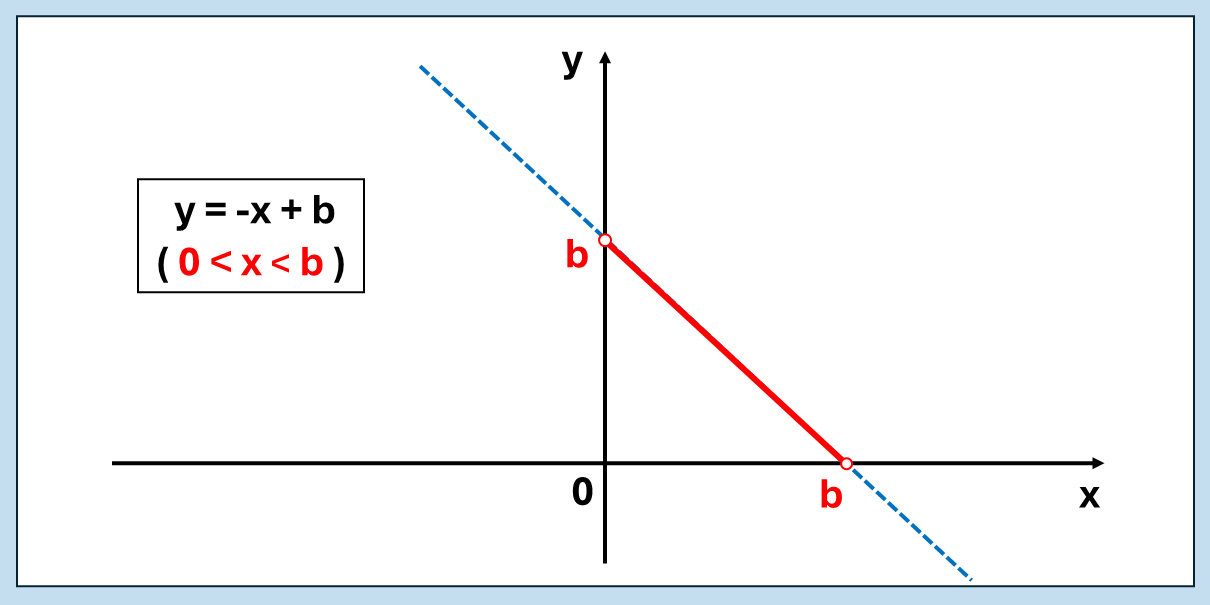
上のグラフが単複の資金配分[ y = -x + b ］を表したグラフです。

ここで１つ重要な条件があります。
単勝式に賭ける金額x円（または複勝式に賭けるy円）には下限値と上限値があることです。

すなわち、下限値は0円（単勝式を買わない）で上限値はb円（資金全額を単勝式に充てて、複勝式を買わない）です。ただし、今回は単複同時に買う場合を想定していますので、xの範囲としては０とbを含まず[ 0 < x < b ]となります。

ですから、上のグラフのうち、実質的に単複の資金配分に関係する部分としては赤実線の部分のみです。

では、ここで「ベストな資金配分」とは何かを定義します。

「ベストな資金配分」の定義

以下の条件をいずれも満たすことができる資金配分（以下「M」とする）のこと

①単勝式の払戻金と複勝式の払戻金の合計額が最大になること
②単複を勝った馬が２着または３着だった場合に、複勝式の払戻金が単複に賭けた合計額を上回っている（回収率が100%を越えている）こと

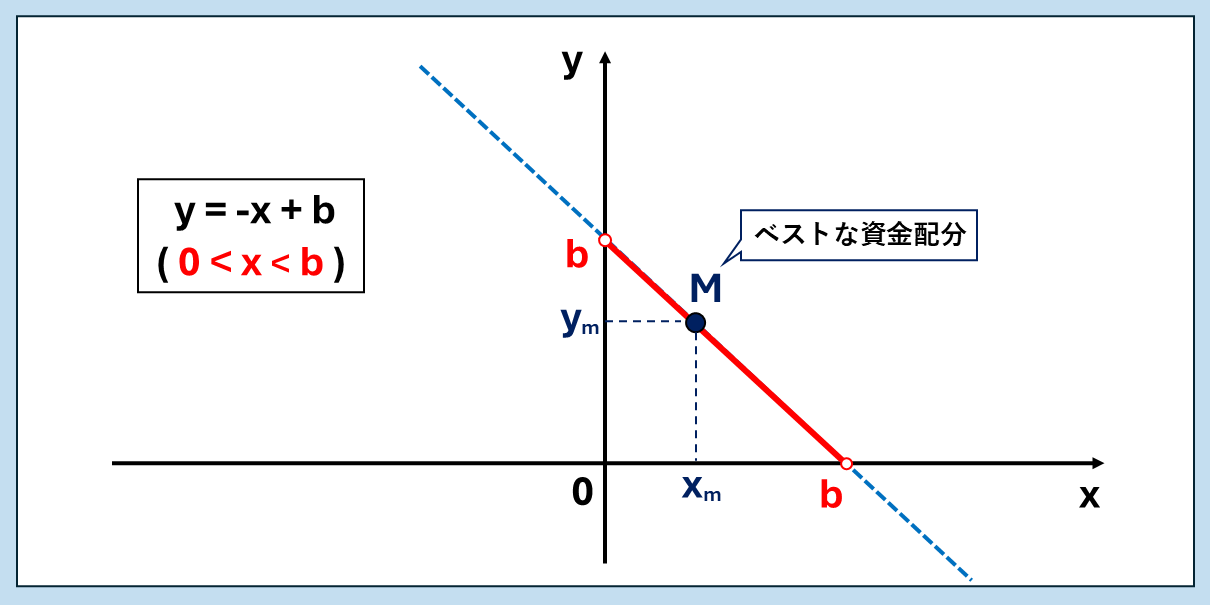
次に、ベストな資金配分Mの座標を以下のように表すこととします。

xmは単勝式に賭ける金額、ymは複勝式に賭ける金額です。
このMは、先ほど説明したとおり１次関数[ y = -x + b ］のグラフ上に存在しますので、

という数式が成り立つことになります。
再確認ですが、この数式の中の「b」は単複を買うための資金の総額を表しています。例えば、資金1,000円を使って単複を買う場合には、[ ym = -xm + 1000 ]という式になるわけです。

お分かりでしょうか？
「ベストな資金配分」とは、１次関数[ y = -x + b ］のグラフ上で動く点Mであり、上で定義した２つの条件を満たす点Mの座標（ xm , ym )を割り出せた時に初めて「ベストな資金配分」を知ることができるのです。

ベストな資金配分には単複のオッズが必要

ここまで単複の資金配分が１次関数であることを解説してきました。

実際に馬券を買う場合には、この１次関数を使ってベストな資金配分M（ xm , ym )を割り出す必要があるのですが、そのためにはまだ足りないものがあります。
それは、単勝式と複勝式の各オッズです。

オッズとは、馬券の購入金額に対してどのくらいの倍率で払戻金が得られるかを表す数値です。例えば、オッズが２倍の馬券を1,000円分購入した場合、その馬券が的中すると1,000円の２倍、つまり2,000円の払戻金が得られるというわけです。
オッズについては、以下の記事で詳しく解説しています。

単勝式にx円を賭けた時に、または、複勝式にy円を賭けた時に、それぞれの馬券が当たるとどのくらいの払戻金が得られるのかを知らなければ、ベストな資金配分を割り出すことはできません。
複勝式にお金を賭けすぎると払戻金が少なくなりますし、逆に単勝式にお金を賭けすぎると複勝式しか当たらなかった時に収支がマイナスになってしまいます。これを防ぐには、「どのくらい買うとどのくらいの払戻金になるのか」を事前に把握しておくしかありません。

そこで、オッズの登場です。
単複を買いたい馬の単勝式のオッズをt、複勝式のオッズをfとすると、ベストな資金配分Mで単複を買った場合の払戻金はそれぞれ次のように表されます。

これで払戻金も計算できるようになりました。

一次関数グラフを使ってベストな資金配分を考える

それでは、「ベストな資金配分」の定義の「①単勝式の払戻金と複勝式の払戻金の合計額が最大になること」について考えてみましょう。

ここで大事な前提条件になるのが、先にも述べたとおり、基本的に複勝式のオッズよりも単勝式のオッズのほうが高くなる、ということです。

すなわち、

という関係性になります。

ですから、単複を買った馬が１着になるケースを想定するなら、できる限り単勝式の方に多くの資金を配分するべき、ということになります。

では、「できる限り」とは具体的にどのような条件でしょうか？

それはズバリ、「ベストな資金配分」の定義の「②単複を勝った馬が２着または３着だった場合に、複勝式の払戻金が単複に賭けた合計額を上回っている（回収率が100%を越えている）こと」が条件になります。

先ほども述べましたが、単勝式にお金を賭けすぎると、もし買った馬が２着や３着だった場合に、複勝式の払戻金だけでは資金を回収しきれず、赤字になってしまいます。
したがって、複勝式だけで回収率がギリギリ100%を超えるくらいの資金を残した上で、残りの資金を単勝式に集中投資することが「ベストな資金配分」と言えそうです。

以上を踏まえて、ベストな資金配分Mの条件を不等式で表すと以下のようになります。

上の不等式は、複勝式の払戻金（ym×f）が資金総額（b）よりも大きい、ということを表しています。
さらに、この不等式をymについて変換すると以下のようになります。

つまり、複勝式に賭ける金額（ym）は、資金総額（b）を複勝式のオッズ（f）で割って求めた数より大きくなければならない、ということが言えるわけです。

これをグラフで表すと、以下の図のようになります。

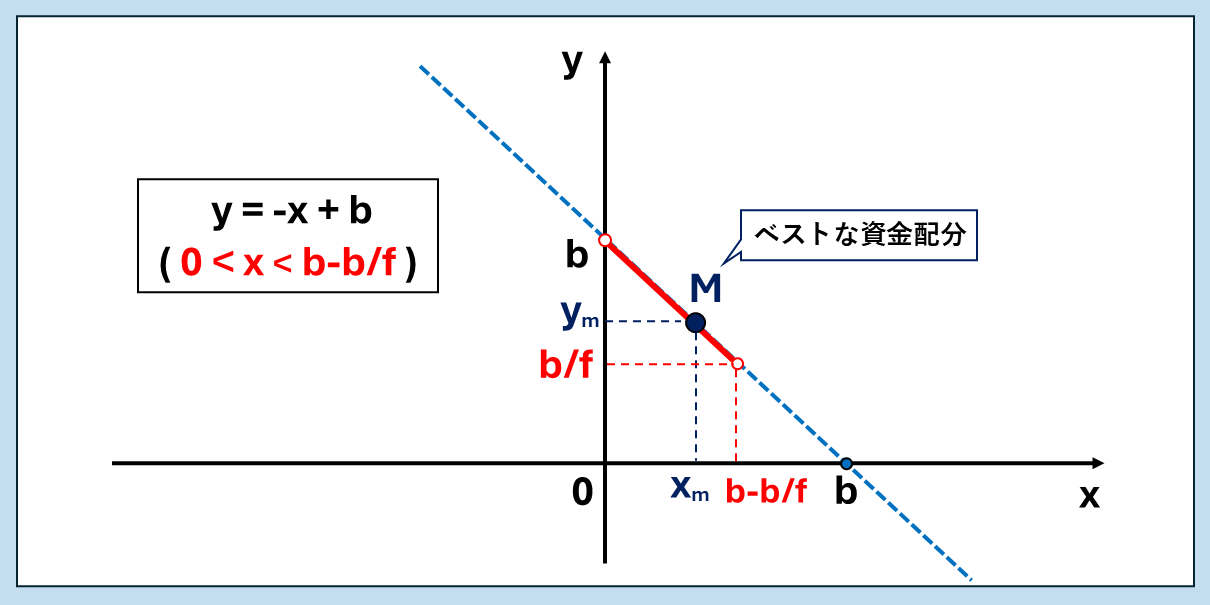
ymはb/fより大きくなければなりませんが、資金総額b円以上の複勝式を買うことはできませんから、ymの上限値はbとなり、以下の不等式が成り立ちます。

そうすると、上のグラフを見てもらえばわかるとおり、xmについても以下の不等式が成り立つことになります。

一次関数[ y = -x + b ］にy=b/fを代入すると、x=b-b/fが求められます。
同様に、y=bを代入すると、x=0が求められますから、xmの下限値は０、上限値はb-b/fだとわかるわけです。

以上より、ベストな資金配分M（ xm , ym ）は、一次関数[ y = -x + b ］のグラフ上で座標（ 0 , b )と座標（ b-b/f , b/f ）の間を移動する点であると言えます。

ベストな資金配分の具体例

数式と記号だけではイメージがわかないと思いますので、具体的な数字を使って資金配分を考えてみましょう。

（具体例）馬Aの単複を買う場合

資金総額（b）：1,000円
馬Aの単勝式オッズ（t）：10.0倍
馬Aの複勝式オッズ（f）：2.0倍

上の例で単勝式に賭ける金額xm円と、複勝式に賭ける金額ym円を考えます。

まず、xmの範囲を先ほどの不等式を使って求めます。
b=1000、f=2ですから

すなわち、馬券は100円単位で買うので、馬Aの単勝式は最低100円、最高400円を賭けることになります。

次に、ymの範囲を同様に不等式を使って求めます。

すなわち、馬Aの複勝式は最低600円、最高900円を賭けることになります。

なお、ymはxmの一次関数で、以下の数式で表せます。

したがって、xmとymの組み合わせをまとめると、以下の表のようになります。

単勝式に賭ける金額 （xm）	複勝式に賭ける金額 （ym）	馬Aが１着だった場合の払戻金	馬Aが２着or３着だった場合の払戻金	資金配分の比率 （xm:ym）
100円	900円	2,800円	1,800円	１：９
200円	800円	3,600円	1,600円	１：４
300円	700円	4,400円	1,400円	１：2.3
400円	600円	5,200円	1,200円	１：1.5

先ほども述べたように、より多くの払戻金を得ようとするなら、できるだけ多くの資金を単勝式に配分するべきです。上の表を見ると、馬Aが１着になるケースでは、単勝式に最高額の400円を賭けた場合に払戻金が最大（5,200円）となっていることがわかります。

一方、馬Aが２着や３着になるケースでは、単勝式はハズレで複勝式のみ的中となりますので、当然ながら、複勝式に最高額の900円を賭けた場合に払戻金が最大（1,800円）となります。

このように、単複を買った馬が１着になるのか、それとも２着や３着になるのかによってベストな資金配分は変わってきますし、１着になる確率と２着や３着になる確率を比べてどちらが高いのかによって、本来は資金配分を変えるべきなのです。

記事の冒頭で、単複の資金配分の比率としては、単勝式１に対して複勝式２～４くらいが一般的によいとされていることをお伝えしました。
上の表を見ると、確かにこの比率であれば結果がどちらに転んでもそこそこの払戻金が得られそうですが、もし単複を買う馬が１着になりそうなら単勝式１に対して複勝式1.5、２着や３着になりそうなら単勝式１に対して複勝式９という比率にするほうが、より理想的な資金配分になるわけです。

オッズがベストな資金配分に与える影響

さきほどの具体例は、あくまで１例に過ぎないのであって、単複を買う馬が人気馬なのか人気薄の馬なのかによって、言い換えると、単勝式と複勝式の各オッズがどのような値かによってもベストな資金配分は変わってきます。

例えば、先ほどの馬Aの例で、単勝式オッズ（t）が5.0倍、複勝式オッズ（f）が1.2倍の人気馬だった場合、ベストな資金配分は以下の表のようになります。

単勝式に賭ける金額 （xm）	複勝式に賭ける金額 （ym）	馬Aが１着だった場合の払戻金	馬Aが２着or３着だった場合の払戻金	資金配分の比率 （xm:ym）
100円	900円	1,580円	1,080円	１：９

前の例とは異なり、ベストな資金配分のパターンは単勝式100円、複勝式900円の１通りしかなく、資金配分の比率は１：９という極端に複勝式に偏ったものになっています。そして、的中したとしても、払戻金はそれほど大きな金額になりません。

この場合、もし１着になる確率が相当高いと判断できるなら、複勝式を買わずに単勝式に全資金を投入するほうが得策かもしれません。
そうでなければ、上の資金配分で単複を買うか、単勝式を買わずに複勝式に全資金を投入するしかないでしょう。

同様に単勝式オッズ（t）が20.0倍、複勝式オッズ（f）が5.0倍の人気薄の馬だった場合、ベストな資金配分は以下の表のようになります。

単勝式に賭ける金額 （xm）	複勝式に賭ける金額 （ym）	馬Aが１着だった場合の払戻金	馬Aが２着or３着だった場合の払戻金	資金配分の比率 （xm:ym）
100円	900円	6,500円	4,500円	１：９
200円	800円	8,000円	4,000円	１：４
300円	700円	9,500円	3,500円	１：2.3
400円	600円	11,000円	3,000円	１：1.5
500円	500円	12,500円	2,500円	１：１
600円	400円	14,000円	2,000円	1.5：１
700円	300円	15,500円	1,500円	2.3：１

上の表のとおり、この場合の資金配分は７通りもあり、単勝式に最高額の700円を賭けると、馬Aが１着だった場合には複勝式と併せて15,500円もの払戻金が得られます。
一方で、馬Aが人気薄の馬であることを考えれば、単勝式は100円に抑えておいて、残り900円を複勝式に集中投資して２～３着だった場合の払戻金4,500円を狙いにいくという手もあります。

このように、ベストな資金配分の比率というのはオッズによって大きく左右され、人気薄の馬（オッズが高い馬）に関しては、（よほど自信があれば）複勝式よりも単勝式の方により多くの資金を投入することも可能になるのです。

では、ここであらためて資金配分とオッズの関係を数式で見てみます。

①②いずれの不等式も、上の「一次関数グラフを使ってベストな資金配分を考える」の項で示したものです。

①の不等式の右辺に着目すると、bというのは定数（変化しない値）ですから、fの値が小さくなればなるほど[ b / f ]の値は大きくなり、逆にfの値が大きくなればなるほど[ b / f ]の値は小さくなります。
つまり、複勝式オッズ（f）が下がれば下がるほど複勝式に賭ける金額（ym）は大きくなり、逆にオッズが上がれば上がるほど複勝式に賭ける金額は小さくなるということです。

このことは、上で示した３つの具体例を比較してもらえば、正しい説明であることをご理解いただけるでしょう。

さらに、②の不等式の右辺に着目すると、やはりbは定数ですから、fの値が小さくなればなるほど[ b – b / f ］の値も小さくなり、逆にfの値が大きくなればなるほど[ b – b / f ］の値も大きくなります。
つまり、複勝式オッズ（f）が下がれば下がるほど単勝式に賭ける金額（xm）は小さくなり、逆にオッズが上がれば上がるほど単勝式に賭ける金額は大きくなるということです。

また、②の不等式をfについて変換すると以下のようになります。

単勝式のオッズtと複勝式のオッズfの間には

という関係性がありますので、先ほどのfについての不等式から

という不等式が成り立ち、これをxmについて変換すると

となります。

③の不等式は、②の不等式のfがtに置き換わっただけですから、複勝式オッズと同様に、単勝式オッズ（t）についても下がれば下がるほど単勝式に賭ける金額（xm）は小さくなり、逆にオッズが上がれば上がるほど単勝式に賭ける金額は大きくなるということが言えるのです。

まとめ

長々と説明してきましたが、今回の内容をまとめると、次のようになります。

単複の「ベストな資金配分」とは

・マイナス収支にならない範囲で払戻金が最大化する資金配分を見つけること
・資金配分の目安は、単複を買うための資金の総額（b円）と買いたい馬の複勝式オッズ（f倍）で以下のとおり計算が可能
　0 < （単勝式に賭ける金額） < b – b / f
　b / f < （複勝式に賭ける金額） < b
・単複を買いたい馬のオッズや勝つ確率（推定）によって資金配分の比率を変えることが重要
・オッズが低い馬（人気馬）は複勝式に、オッズが高い馬（人気薄の馬）は単勝式により多くの資金を配分するのがセオリー
・勝つ確率が高そうな人気馬であれば、単複ではなく単勝式だけ買う方が得策
・勝つ確率が低そうな人気薄の馬であれば、セオリーを外れて複勝式に集中投資することも要検討

今回は、中学校の数学で習う「１次関数」を使って単複の資金配分を計算する試みでした。
ですが、数式やグラフは一切忘れていただいて構いません。

それよりも、これから単複を買う時には、上で示した「ベストな資金配分」の考え方を踏まえたうえで、馬のオッズや勝つ確率を十分に考慮しながら適切な資金配分で馬券を買えるようになることが重要です。

そうすれば、きっと今までよりも競馬を楽しむことができるようになるでしょう。

参考書籍

「やさしい中学数学　改訂版　電子版」（きさらぎひろし著、Gakken）

Amazonのアソシエイトとして、競馬ディスカバリーブログは適格販売により収入を得ています。