
数学の第2回は、式の計算。
今回は、「なぜ逃げ馬は”外枠”が有利なのか」について、中学生でも理解できるよう分かりやすく解説していきます。
「内枠」と「外枠」

記事のタイトルを見て「本当なの?」と不思議に思った競馬ファンも少なくないかもしれませんが、本当に外枠の逃げ馬が有利なのかどうか、中学レベルの数学を使って検証しようというのがこの記事の趣旨になります。
その前に、競馬に詳しくない方は「外枠(そとわく)」の意味がわからないかもしれませんので、ここで説明します。
そもそも、「外枠」の対義語として「内枠(うちわく)」という言葉もあります。
それぞれ「外側の枠」と「内側の枠」という意味ですが、では「枠(わく)」とは何かというと、競馬のレースで競走馬がスタートする時に入るゲート(上図)のことです。
ゲートには1頭ずつ入る部屋があって、各部屋に番号が振られています。これをゲート番号といいます。上の図では1番から18番までのゲート番号が振られています。
日本の競馬も海外の競馬も、レースごとに馬番(号)という通し番号が各出走馬に振られます。出走頭数が18頭であれば、1番から18番まで馬番が振られます。
日本競馬では、馬番がそのままゲート番号となります。
ですから、馬番が1番の馬はゲート番号1番の部屋からスタートするわけです。
ちなみに、海外競馬ではほとんどの場合、馬番とは別にゲート番号が振られます。
例えば、馬番1番の馬がゲート番号8番の部屋からスタートするような状況が起こるわけです。日本の競馬ファンが海外競馬を見る時に一番混乱するのはこの点でしょう。
長い説明になりましたが、では「内枠」と「外枠」が何を意味するのかというと、「内枠」はゲート番号(日本であれば馬番)が小さい方のゲートに入ることで、逆に、「外枠」はゲート番号が大きい方のゲートに入ることをいいます。
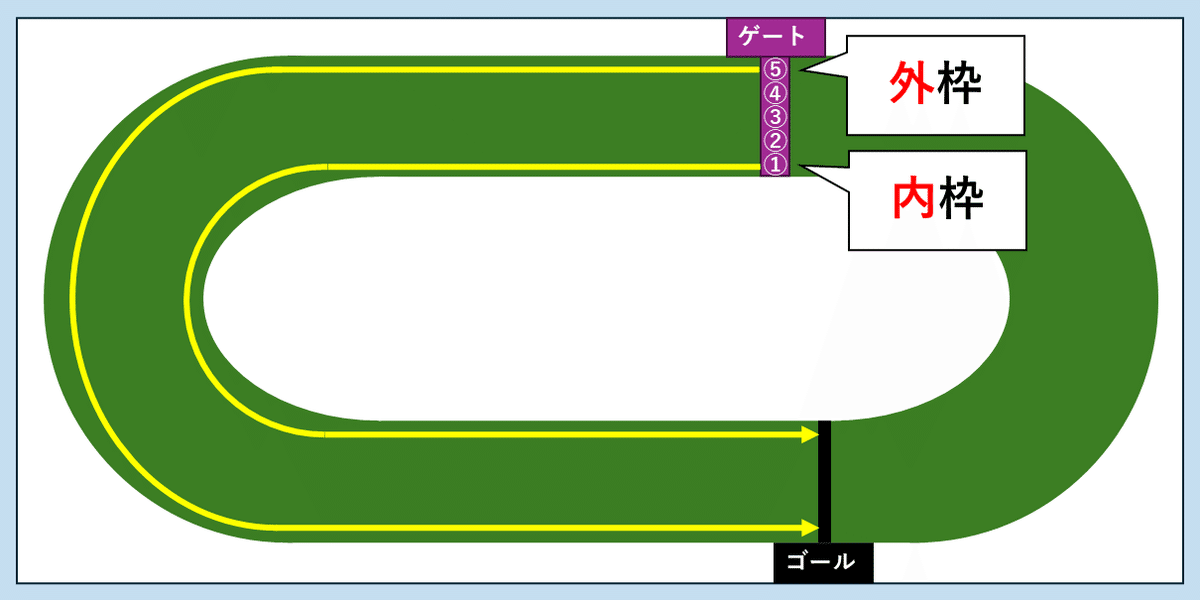
上の図は競馬場のトラック(コース)を上から見た模式図で、楕円形のコースの上側にゲート(紫色)、下側にゴール線(黒色)を描いています。
左回り(反時計回り)のコースなので、黄色い線と矢印で示したような経路で競走馬がゲートからゴールまで走ることになります。
ゲート番号はコースの内側から外側に向かって順番に振られていきます。
上の図の例で行くと、一番内側のゲート番号が1番、一番外側のゲート番号が5番です。
つまり、ゲート番号が小さければ小さいほどコースの内側からスタートし、逆に大きければ大きいほどコースの外側からスタートすることになるわけですので、ゲート番号が小さい方を「内枠」、大きい方を「外枠」というわけです。
上の図の黄色い線を見てもらえばわかるとおり、内枠の馬よりも外枠の馬の方が長い距離を走ることになりますので、一般的に内枠の馬に比べて外枠の馬は不利と考えられています。
内枠と外枠でどのくらい走る距離が違うのか
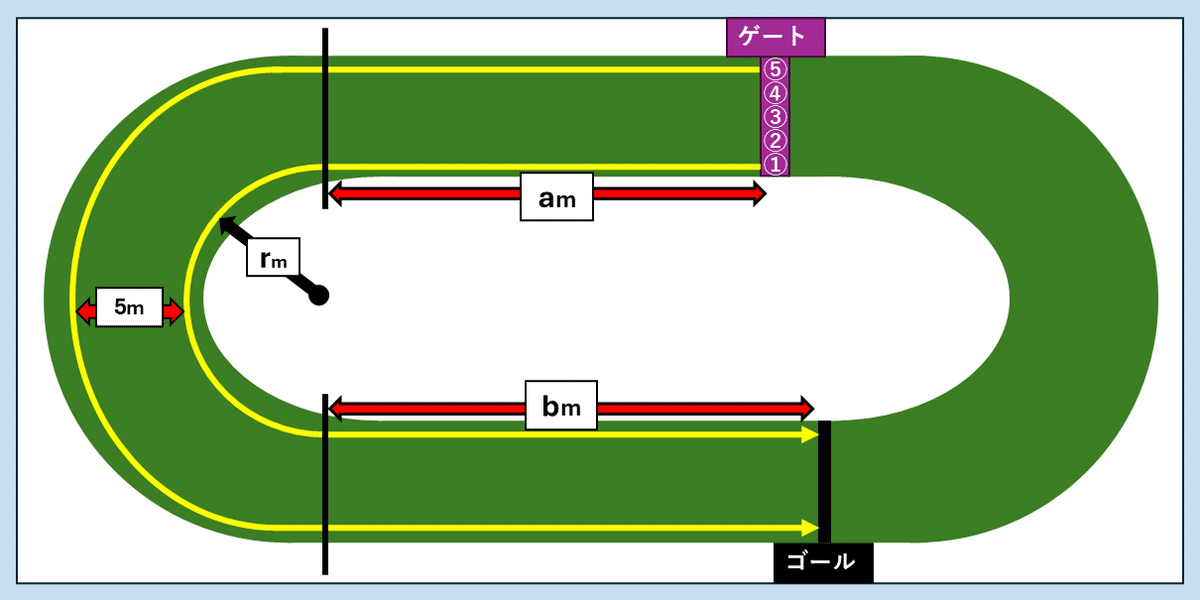
では、内枠の馬と外枠の馬でどのくらい走る距離が違うのか、上の図を使って実際に計算してみましょう。
まず馬が走るコースですが、ゲートからスタートしてaメートルの直線を走り、左回りに大きくカーブ(コーナー)を曲がって、最後の直線をbメートル走ってゴールとなります。
なお、ゲート番号1番(内枠)の馬と5番(外枠)の馬の間の距離は5メートルで、コーナーの内周の半径はrメートルです。
このときの1番の馬と5番の馬の走る距離を計算する式は、それぞれ以下のようになります。
(1番の馬が走る距離)=a+b+πr
(5番の馬が走る距離)=a+b+π(r+5)
※πは円周率(3.14)のこと。(円周の長さ)=(直径)×(円周率)なので、(半円の円周の長さ)=(円周の長さ)÷2=(半径)×(円周率)
直線部分の距離は(a+b)メートルで1番の馬も5番の馬も同じですが、コーナー部分の距離は1番よりも5メートル外を走る5番の方が長くなります。
では、5番の馬が走る距離と1番の馬が走る距離の差を求めてみましょう。
(5番の馬が走る距離)-(1番の馬が走る距離)
={a+b+π(r+5)}- (a+b+πr)
=a+b+πr+5π-a-b-πr
=5π
=5×3.14
=15.7(メートル)
ということで、5番(外枠)の馬の方が1番(内枠)の馬よりも15.7メートルも長い距離を走ることになるわけです。
15メートルがどのくらいの距離かというと、馬と馬の縦関係の距離を「何馬身(ばしん)」という用語で表しますが、1馬身、つまり馬1頭分の長さが大体2.5メートルくらいですので、15メートルの差というのは6馬身差に該当します。
つまり、コーナーを曲がり切って最後の直線に差しかかった時点で、5番の馬は1番の馬に6馬身差をつけられている計算になるのです。競馬ファンの方であれば、この距離の差がどのくらい大きな差なのかご理解いただけたのではないでしょうか。
中央GⅠレースにおける逃げ馬の枠番別成績

それでは、いよいよ今回の本題について解説していきます。
「内枠」と「外枠」については先ほど解説したとおりですが、では、「逃げ馬」とは何なのでしょうか。
これは、その名のとおり「レースで逃げる馬」のことで、競馬でいう「逃げる」とは先頭でレースを走ることです。先頭のままでゴールできれば「逃げ切った」といいますし、先頭でゴールできなくても2着や3着に入れば「逃げ粘った」といいます。
一方、レース序盤は先頭におらず、レース終盤になって初めて先頭に立った馬は「逃げ馬」と言いません。
要するに、最終的な着順に関係なく、レース序盤から先頭に立って走る馬のことを「逃げ馬」というわけです。
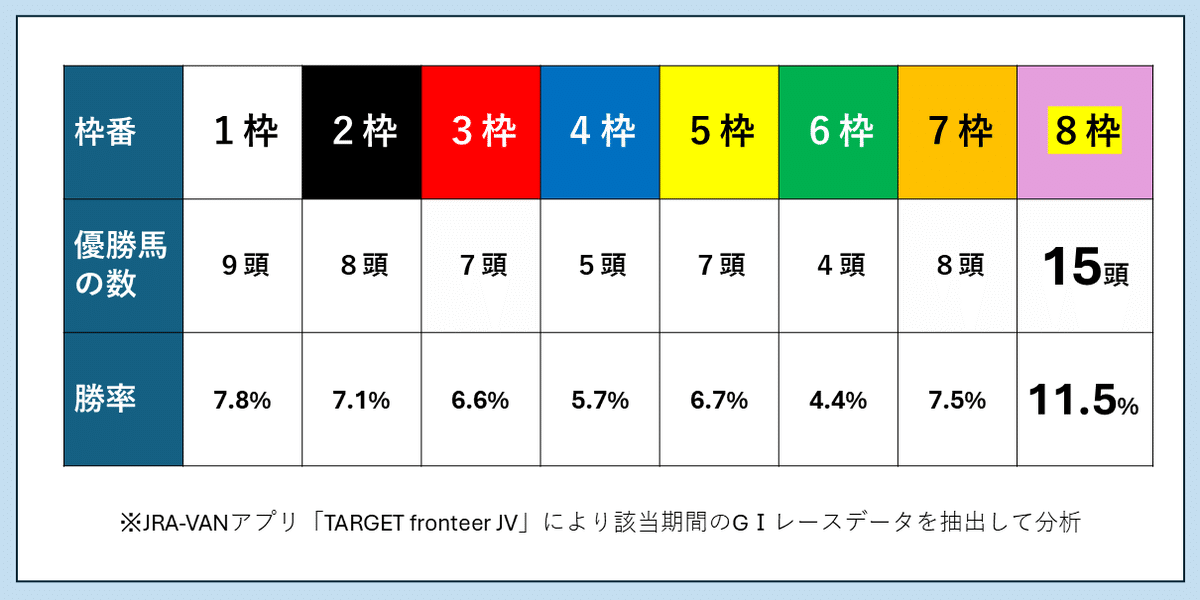
逃げ馬に関するデータを調べてみると、距離的に不利なはずの外枠からスタートした逃げ馬の方が、内枠や真ん中の枠からスタートした逃げ馬よりも好成績を残していることがわかりました。
上の図は、1986年から2024年まで(39年間)に中央競馬で開催された平地のGⅠレースにおける逃げ馬の枠番別成績を示しています。
「GⅠレース」というのは、競馬レースの中で最もグレードの高いレースで、最もハイレベルな馬たちが走るレースです。ごまかしが効かない実力勝負のレースなので、正確に傾向を分析するためには最適なレースと言えます。
「枠番」とは、先ほど説明した馬番とは別に各出走馬に振られる番号のことで、1枠から8枠まで(出走頭数が6頭や7頭なら6枠や7枠まで)の番号が振られます。
枠番は馬番とセットで振られるので、馬番が決まれば自動的に枠番も決まります。馬番と同様にゲートの内側から外側に向かって順に枠番が振られるので、1枠が内枠、8枠が外枠と見ることができます。
上の図のとおり、なんと優勝馬の頭数、勝率ともに8枠(外枠)の逃げ馬が他の枠番の逃げ馬たちよりも圧倒的に好成績を収めています。
最も優勝馬が少ない枠番(6枠)と比較して、3倍以上となる15頭もの馬が8枠から逃げて優勝しています。
また勝率に関しては、11.5%、つまり10頭に1頭以上の割合で8枠の逃げ馬がGⅠレースを優勝しているというのです。
競馬ファンの方は、この真実にお気づきだったでしょうか?
データを見て初めて気づいた方も多いかもしれません。
実は、このデータを象徴するようなGⅠレースが2つあります。
しかも、2つとも同じ逃げ馬が勝ったレースです。
1つ目は1995年のGⅠ皐月賞、もう1つは同じく1995年のGⅠ日本ダービー。勝ったのは、いずれもサニーブライアンという逃げ馬です。
馬番と枠番は抽選で決まりますので、外枠になるのかどうかは、はっきりいうと”運”です。
そんな中で、サニーブライアンは皐月賞、日本ダービーともに8枠18番という大外枠に入ってしまいます。
運が悪いとしか言いようがない気がしますが、なんとサニーブライアンはその2つのGⅠレースを逃げ切ってしまったのです。
ぜひ2つのレースを最初から最後まで見ていただきたいのですが、注目していただきたいのはスタート直後のサニーブライアンの動きです。
この動きに、実は先ほどのデータの秘密が隠されています。
外枠の逃げ馬が勝つ秘訣はスタートダッシュにある
先ほど内枠と外枠でどのくらい走る距離が違うのかについて解説しましたが、実際の競馬では外枠の馬がコースの内側を走ることもありますし、その逆の場合もあります。
先ほど紹介した1997年の皐月賞と日本ダービーのレースを見ると、いずれのレースでも、大外枠からスタートしたサニーブライアンはゲートを出てわずか100~200メートルを走る間に一気に内側に切れ込んで先頭に立っています。
そうです。コースの外側を走ることが距離的に不利だと最初からわかっているのですから、外枠から逃げたい馬はスタートダッシュを決めてすぐ内側に進路を確保するべきなのです。
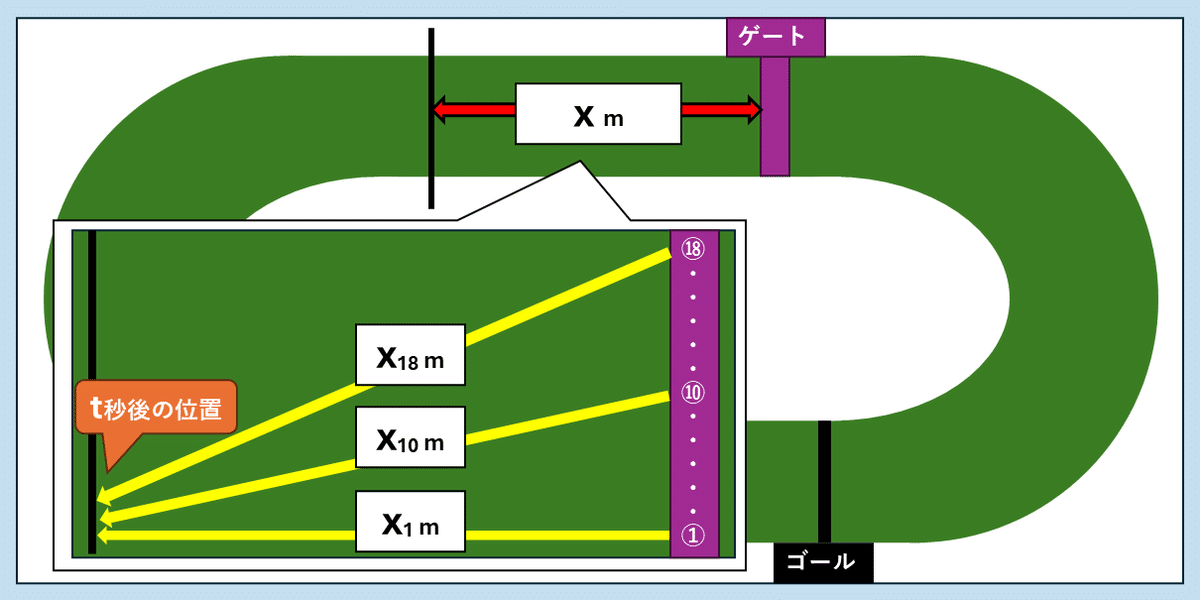
上の図は、先ほどの左回りの競馬場のコースで18頭の馬がゲートからゴールまで目指すレースを模式的に描いたものです。
この図で、逃げ馬がゲートからxメートルの地点で先頭に立ちたい場合に、1番(内枠)の馬が走る距離(x1)、10番(真ん中)の馬が走る距離(x10)、18番(外枠)の馬が走る距離(x18)を計算する式は、それぞれ下の図のとおりです。
ただし、ゲートの長さは1頭につき1mの長さがあるものとします。

1番の馬は当然真っすぐ走るだけですから、xメートル走れば先頭に立てます。
一方、10番や18番の馬は、ゲートを出たあとコースの内側に向かって斜めに走る分だけ1番の馬よりも長い距離を走ることになります。この距離の計算は、直角三角形の3辺の比、いわゆる「三平方の定理」を使って上図のように解くことができます。
では、内枠と外枠で逃げ馬の走る距離にどのくらいの差が生まれるのか、この計算式を使って見比べてみましょう。
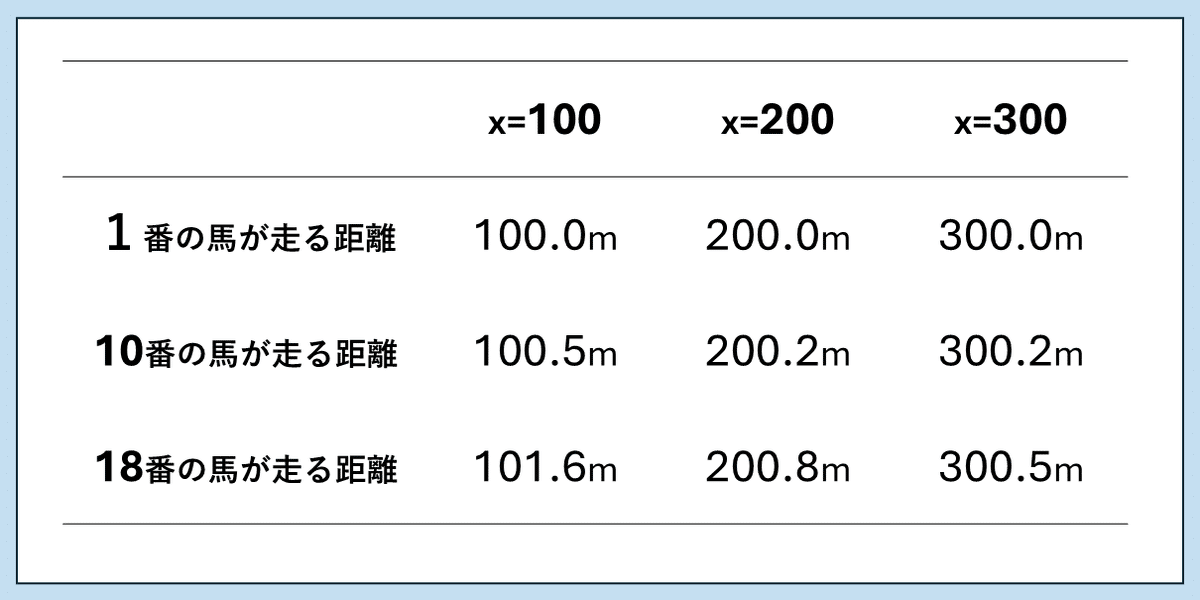
上の図は、x=100(メートル)、x=200(メートル)、x=300(メートル)のそれぞれの場合について、1番と10番と18番の各逃げ馬が先頭に立つまでにどのくらいの距離を走る必要があるのか比較した表です。
どうでしょうか?
思ったよりも走る距離の差が少ないと感じませんか?
イメージ的に10メートル、20メートルは違うような気がしますが、実際に計算してみると最大でも1.6メートル程度の差しかありません。
ゲートから300メートル地点で先頭に立つ場合(x=300)に関しては、内枠と外枠でほぼ走る距離に差がない印象です。
これを踏まえた上で、もう1歩踏み込んだ計算をしてみます。
高校の物理で「加速度」というものを勉強しますが、ここでは中学生でも理解できるように、あえて詳しい説明は省略します。
加速度とは、簡単にいうと「どのくらいスピードに勢いがついているか」を数値で表したものです。
速度は「時速60キロメートル」というふうに表しますが、ある時点で時速60キロメートルだったとしても、スピードに勢いがあれば1秒後には時速61キロメートルに速度が上がりますし、逆に勢いがなければ時速59キロメートルに下がってしまいます。
このように、速度とは別に加速度という数値を使うことで、馬のスピードをより正確に把握することができるのです。
加速度は、以下の計算式で求められます。
これも高校の物理で勉強する内容ですので、「ああ、そうなんだ」くらいに思っていてください。
(加速度) = (距離) × 2 ÷ (時間)^2
※「^2」は二乗の意味
では、先ほどの例を使って、ゲートからxメートル地点までt秒で到達する場合の加速度を計算してみます。
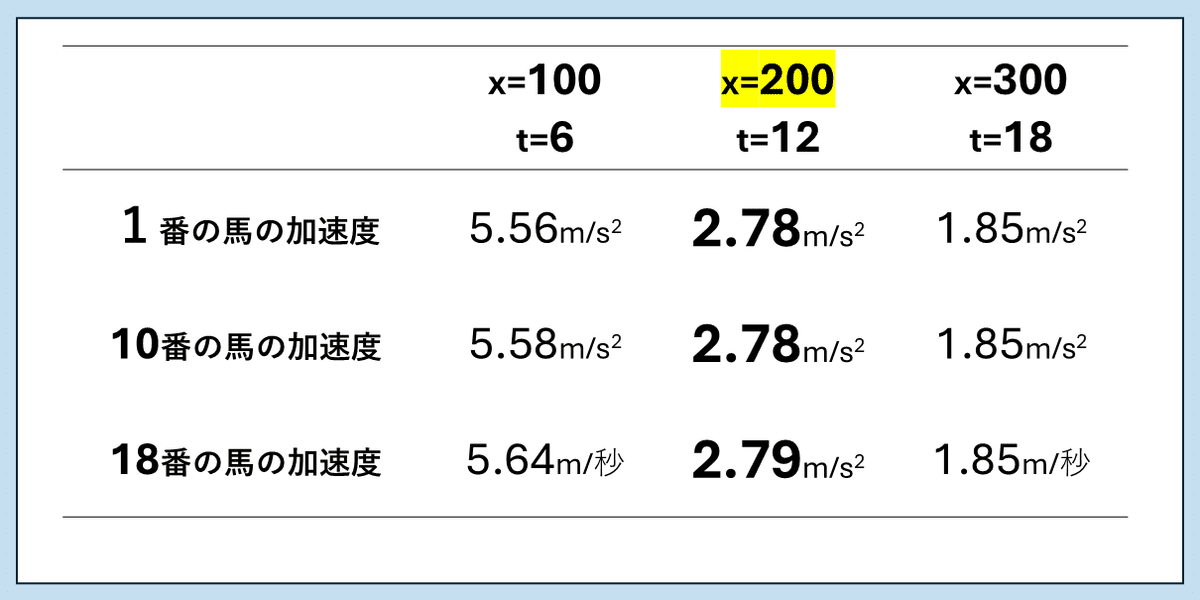
上の図は、x=100(メートル)、x=200(メートル)、x=300(メートル)のそれぞれの場合について、1番と10番と18番の各逃げ馬がスタートからt秒後に先頭に立つために必要な加速度を比較した表です。
tの値に関しては、100mあたり6秒(競馬レースの標準的なラップタイム)という数値を採用しました。
細かい数値は気にしなくて結構ですが、注目していただきたいのはx=200の加速度です。
ゲートから200メートルの地点で先頭に立つ場合は、内枠であろうと外枠であろうと、ほぼ同じ加速度で先頭に立つことができるのです。
これも高校の物理で勉強することなのですが、加速度というのはその物体に働いている力の大きさに比例します。
競走馬で言えば、馬が頑張って力を出せば出すほど加速度が大きくなるです。
すなわち、スタートから200mくらいで先頭に立つのであれば、外枠の馬であっても内枠の馬とほぼ同じ力で逃げることができるわけです。
逆に、スタートから100mくらいで先頭に立とうと思うと、外枠の馬は内枠の馬よりも大きな力(加速度)が必要になりますので、のちのち体力的に厳しくなります。
そう考えると、大外枠のサニーブライアンがゲートを出て100mから200mの間に先頭に立った皐月賞や日本ダービーは理にかなった戦法だったといえるでしょう。
ただ、これまで見てきた数学的・物理学的な検証が「なぜ逃げ馬は”外枠”が有利なのか」を完全に証明しているわけではありません。なぜなら、今回の検証は「外枠の逃げ馬が内枠の逃げ馬よりも不利になるとは限らない」ことを示しただけだからです。
なぜ内枠の逃げ馬よりも外枠の逃げ馬が有利なのか。この点については、別の機会にさらなる検証を行ってみることとします。
参考書籍
「競走馬の科学 速い馬とはこういう馬だ」(JRA競走馬総合研究所著、講談社)
「サラブレッドの生物学 競走馬の速さの秘密」(『生物の科学 遺伝』編集部編、NTS)
「やさしい高校物理(物理基礎) 改訂版 電子版」(堀輝一郎著、学研プラス)
「やさしい中学数学 改訂版 電子版」(きさらぎひろし著、Gakken)
